Как сжать бесконечность? Один шаг за границу возможного — и формула, которую забыли на 70 лет
NewsMakerОн взял хаос, симметрию и терпение. И ждал, пока сойдутся звёзды.

Математик Боаз Клартаг добился большого прорыва в одной из старейших задач геометрии: как максимально плотно размещать сферы в пространстве произвольной размерности. Несмотря на абстрактный характер, задача имеет практическое значение — от криптографии и сжатия данных до передачи информации и устойчивого кодирования.
В привычных трёх измерениях самый компактный способ упаковки давно придуман: шарообразные объекты, выложенные по принципу апельсиновой пирамиды, занимают около 74% объёма. Ещё в XVII веке это предположил Иоганн Кеплер, и лишь в 1998 году гипотеза была окончательно доказана. Но как только мы выходим за пределы трёх измерений, ситуация резко усложняется — интуиция больше не работает, а геометрия очень уж туго поддаётся анализу.
До недавнего времени точные решения существовали лишь для 8- и 24-мерных пространств, где можно было применить мощные инструменты теории симметрий. В остальных случаях учёные годами двигались малыми шагами, предлагая приближённые варианты без серьёзных подвижек.
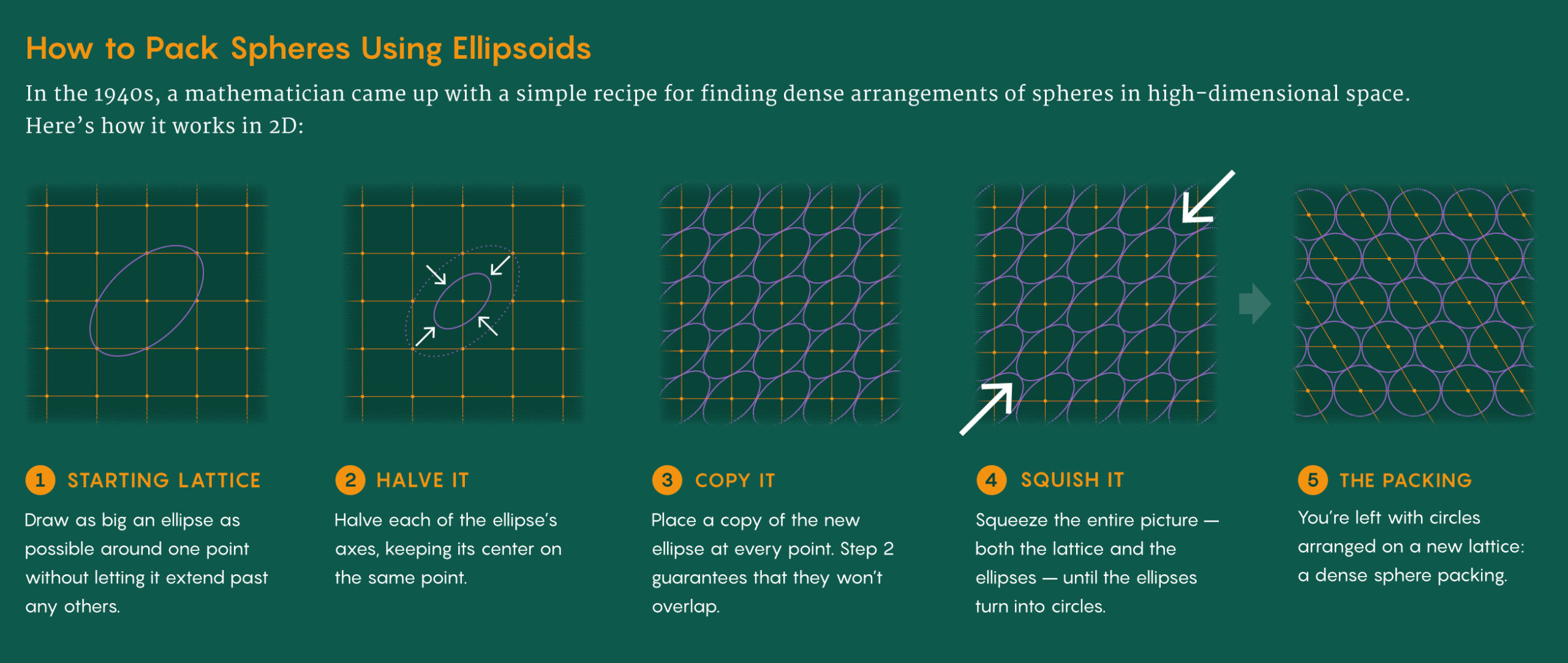
Новый подход базируется на малоизвестной идее, предложенной ещё в 1947 году Клодом Роджерсом: начинать не с фиксированной решётки, а с эллипсоида — деформированной сферы, вписанной между точками. Смысл в том, чтобы подобрать такую форму, которая касается, но не пересекает ближайших точек решётки. Но в высоких измерениях выбор формы становился почти невозможным из-за бесконечного числа направлений растяжения, и метод надолго забыли.
Клартаг решил вернуться к этой идее, но применил к ней инструменты из своей области. Он разработал стохастический алгоритм , который "раздувает" эллипсоид в разных направлениях, останавливая его рост там, где он начинает касаться точек решётки. Благодаря многократным итерациям формируются разные варианты упаковки, а в среднем объём фигуры оказывается значительно больше, чем в классическом подходе Роджерса.
Результаты превзошли ожидания: удалось успешно доказать, что новая методика позволяет достичь плотности, в десятки и даже сотни раз превышающей прежние значения. В пространстве с 100 измерениями, например, можно разместить примерно в 100 раз больше сфер, чем позволяли традиционные решётки.
Важно, что это не просто улучшение существующего метода. Работа Клартага фактически вернула в научную повестку геометрические стратегии, которые считались бесперспективными. Она также вновь активизировала дискуссию о том, какой подход лучше в высоких размерностях: строго упорядоченные конфигурации или же модели с меньшей симметрией. Все данные говорят в пользу структурированного, симметричного подхода.
По мнению некоторых экспертов, новая упаковка приближается к теоретическому пределу. Другие считают, что потенциал метода ещё не исчерпан. Так или иначе, это крупнейший шаг вперёд за десятилетия.
У задачи есть и прикладное измерение. При передаче данных через зашумлённые каналы — например, в квантовых коммуникациях или глубококосмической связи — важно кодировать информацию так, чтобы плотность была максимальной, а ошибки минимальными. По сути, это та же задача размещения сфер. И хотя предложенный метод пока не адаптирован для практики, он уже вызвал интерес у специалистов по теории информации.
Сам Клартаг надеется, что его работа послужит толчком к объединению двух направлений — теории решёток и родной для него выпуклой геометрии. По его мнению, синтез способен раскрыть новые горизонты, и его собственный успех — убедительное тому подтверждение.

Математик Боаз Клартаг добился большого прорыва в одной из старейших задач геометрии: как максимально плотно размещать сферы в пространстве произвольной размерности. Несмотря на абстрактный характер, задача имеет практическое значение — от криптографии и сжатия данных до передачи информации и устойчивого кодирования.
В привычных трёх измерениях самый компактный способ упаковки давно придуман: шарообразные объекты, выложенные по принципу апельсиновой пирамиды, занимают около 74% объёма. Ещё в XVII веке это предположил Иоганн Кеплер, и лишь в 1998 году гипотеза была окончательно доказана. Но как только мы выходим за пределы трёх измерений, ситуация резко усложняется — интуиция больше не работает, а геометрия очень уж туго поддаётся анализу.
До недавнего времени точные решения существовали лишь для 8- и 24-мерных пространств, где можно было применить мощные инструменты теории симметрий. В остальных случаях учёные годами двигались малыми шагами, предлагая приближённые варианты без серьёзных подвижек.
Новый подход базируется на малоизвестной идее, предложенной ещё в 1947 году Клодом Роджерсом: начинать не с фиксированной решётки, а с эллипсоида — деформированной сферы, вписанной между точками. Смысл в том, чтобы подобрать такую форму, которая касается, но не пересекает ближайших точек решётки. Но в высоких измерениях выбор формы становился почти невозможным из-за бесконечного числа направлений растяжения, и метод надолго забыли.
Клартаг решил вернуться к этой идее, но применил к ней инструменты из своей области. Он разработал стохастический алгоритм , который "раздувает" эллипсоид в разных направлениях, останавливая его рост там, где он начинает касаться точек решётки. Благодаря многократным итерациям формируются разные варианты упаковки, а в среднем объём фигуры оказывается значительно больше, чем в классическом подходе Роджерса.

Результаты превзошли ожидания: удалось успешно доказать, что новая методика позволяет достичь плотности, в десятки и даже сотни раз превышающей прежние значения. В пространстве с 100 измерениями, например, можно разместить примерно в 100 раз больше сфер, чем позволяли традиционные решётки.
Важно, что это не просто улучшение существующего метода. Работа Клартага фактически вернула в научную повестку геометрические стратегии, которые считались бесперспективными. Она также вновь активизировала дискуссию о том, какой подход лучше в высоких размерностях: строго упорядоченные конфигурации или же модели с меньшей симметрией. Все данные говорят в пользу структурированного, симметричного подхода.
По мнению некоторых экспертов, новая упаковка приближается к теоретическому пределу. Другие считают, что потенциал метода ещё не исчерпан. Так или иначе, это крупнейший шаг вперёд за десятилетия.
У задачи есть и прикладное измерение. При передаче данных через зашумлённые каналы — например, в квантовых коммуникациях или глубококосмической связи — важно кодировать информацию так, чтобы плотность была максимальной, а ошибки минимальными. По сути, это та же задача размещения сфер. И хотя предложенный метод пока не адаптирован для практики, он уже вызвал интерес у специалистов по теории информации.
Сам Клартаг надеется, что его работа послужит толчком к объединению двух направлений — теории решёток и родной для него выпуклой геометрии. По его мнению, синтез способен раскрыть новые горизонты, и его собственный успех — убедительное тому подтверждение.