От наутилуса до Захи Хадид: учёные нашли формы без углов в природе и искусстве
NewsMakerИсследование показало неожиданные связи математики с природой.

Группа венгерских исследователей под руководством математика Габора Домокоша сделала открытие, которое способно изменить представление о геометрии, природе и искусстве. Они обнаружили новый тип геометрических форм, названных «мягкими клетками», которые могут полностью заполнять плоскости и трехмерные пространства. Уникальность этих форм заключается в отсутствии углов: в двух измерениях такие клетки имеют всего два угла, соединенных кривыми, а в трех измерениях они вовсе лишены углов.
Работа началась с попытки ответить на вопрос, какое минимальное количество углов может быть у фигуры, способной замостить плоскость без зазоров. Исследователи выяснили, что минимальное число — два. Это противоречит ранее устоявшимся представлениям о том, что замощение невозможно без фигур с тремя углами, таких как треугольники. Дальнейшие исследования привели к разработке математического алгоритма, который позволил преобразовывать классические многогранники в закругленные мягкие формы. Этот алгоритм основывается на теории графов, а именно на гамильтоновых путях, что позволило сгладить углы многогранников и превратить их в новые типы ячеек.
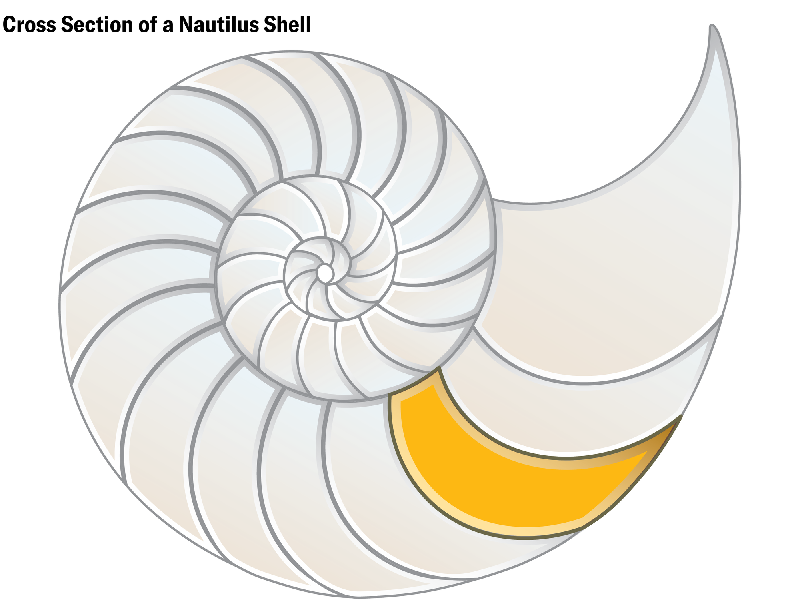
Мягкие клетки оказались не только математическим феноменом. Ученые начали находить такие формы в природе, искусстве и архитектуре. В частности, исследователи обнаружили подобные структуры в раковинах наутилусов и аммонитов. Эти природные формы обладают минимальной энергетической затратностью благодаря отсутствию острых углов. В живых организмах мягкие клетки обеспечивают эффективное заполнение пространства, что можно наблюдать в тканях, клетках крови и других структурах. В архитектуре аналогичные формы использовались в проектах Захи Хадид и других архитекторов, работающих с плавными, органичными линиями.
Работа венгерских исследователей также затронула связь между природой и искусственными объектами. Оказалось, что концепция мягких клеток уже интуитивно применялась в архитектурных проектах. Например, в проекте здания для Cirque du Soleil использовались элементы, которые в математическом описании соответствуют мягким клеткам. Эта находка объединяет искусство, науку и дизайн, показывая, что органичность форм может быть как эстетическим, так и функциональным решением.
Исследование не ограничилось двухмерными клетками. Домокош и его коллеги доказали существование трехмерных мягких клеток, которые могут заполнять пространство без углов. Они нашли примеры таких форм в природе, а также разработали алгоритмы для их создания. Эти формы объединяют в себе плавность линий и способность эффективно заполнять объем, что открывает новые возможности для материаловедения, архитектуры и биологии.

Работа исследователей ставит множество новых вопросов. Например, можно ли создать мягкие клетки, способные заполнять пространство без повторяющихся узоров, как это происходит с апериодическими мозаиками ? Исследование также поднимает тему оптимального заполнения пространства в биологических структурах и искусственных материалах. Несмотря на то что прямых доказательств биологических процессов, связанных с мягкими клетками, пока нет, визуальные совпадения с природными структурами указывают на перспективность этой области.
Исследование мягких клеток уже привлекло внимание ученых из разных областей. Оно объединяет геометрию, биологию и искусство, предлагая новые подходы к изучению пространства и его структуры. Открытие подчеркивает, как природа избегает острых углов, выбирая более плавные, энергоэффективные формы. Это направление обещает стать основой для новых технологий и теорий, которые помогут понять устройство окружающего мира.

Группа венгерских исследователей под руководством математика Габора Домокоша сделала открытие, которое способно изменить представление о геометрии, природе и искусстве. Они обнаружили новый тип геометрических форм, названных «мягкими клетками», которые могут полностью заполнять плоскости и трехмерные пространства. Уникальность этих форм заключается в отсутствии углов: в двух измерениях такие клетки имеют всего два угла, соединенных кривыми, а в трех измерениях они вовсе лишены углов.
Работа началась с попытки ответить на вопрос, какое минимальное количество углов может быть у фигуры, способной замостить плоскость без зазоров. Исследователи выяснили, что минимальное число — два. Это противоречит ранее устоявшимся представлениям о том, что замощение невозможно без фигур с тремя углами, таких как треугольники. Дальнейшие исследования привели к разработке математического алгоритма, который позволил преобразовывать классические многогранники в закругленные мягкие формы. Этот алгоритм основывается на теории графов, а именно на гамильтоновых путях, что позволило сгладить углы многогранников и превратить их в новые типы ячеек.

Мягкие клетки оказались не только математическим феноменом. Ученые начали находить такие формы в природе, искусстве и архитектуре. В частности, исследователи обнаружили подобные структуры в раковинах наутилусов и аммонитов. Эти природные формы обладают минимальной энергетической затратностью благодаря отсутствию острых углов. В живых организмах мягкие клетки обеспечивают эффективное заполнение пространства, что можно наблюдать в тканях, клетках крови и других структурах. В архитектуре аналогичные формы использовались в проектах Захи Хадид и других архитекторов, работающих с плавными, органичными линиями.
Работа венгерских исследователей также затронула связь между природой и искусственными объектами. Оказалось, что концепция мягких клеток уже интуитивно применялась в архитектурных проектах. Например, в проекте здания для Cirque du Soleil использовались элементы, которые в математическом описании соответствуют мягким клеткам. Эта находка объединяет искусство, науку и дизайн, показывая, что органичность форм может быть как эстетическим, так и функциональным решением.
Исследование не ограничилось двухмерными клетками. Домокош и его коллеги доказали существование трехмерных мягких клеток, которые могут заполнять пространство без углов. Они нашли примеры таких форм в природе, а также разработали алгоритмы для их создания. Эти формы объединяют в себе плавность линий и способность эффективно заполнять объем, что открывает новые возможности для материаловедения, архитектуры и биологии.

Работа исследователей ставит множество новых вопросов. Например, можно ли создать мягкие клетки, способные заполнять пространство без повторяющихся узоров, как это происходит с апериодическими мозаиками ? Исследование также поднимает тему оптимального заполнения пространства в биологических структурах и искусственных материалах. Несмотря на то что прямых доказательств биологических процессов, связанных с мягкими клетками, пока нет, визуальные совпадения с природными структурами указывают на перспективность этой области.
Исследование мягких клеток уже привлекло внимание ученых из разных областей. Оно объединяет геометрию, биологию и искусство, предлагая новые подходы к изучению пространства и его структуры. Открытие подчеркивает, как природа избегает острых углов, выбирая более плавные, энергоэффективные формы. Это направление обещает стать основой для новых технологий и теорий, которые помогут понять устройство окружающего мира.